Divide and Conquer

Photo by Florian Olivo on Unsplash

Introduction

In the divide and conquer algorithm, we break(DIVIDE) the problem into smaller sub-problems and solve(CONQUER) those sub-problems individually to ultimately solve the original problem. This algorithm uses recursion to break down and solve the problem.

This algorithm is widely used in computer science in various problems and algorithms. For example, the divide and conquer algorithm is used in Merge Sort, Quick Sort, Binary Search and Karatsuba Algorithm, along with many other algorithms and problems.

Algorithm

The divide and conquer algorithm follows three simple steps:

1. Divide: Divide the problem into sub-problems.
2. Solve: Solve the problem recursively.
3. Merge: Combine the sub-problems to find the solution to the original problem.

Divide and Conquer Algorithm, by Javapoint

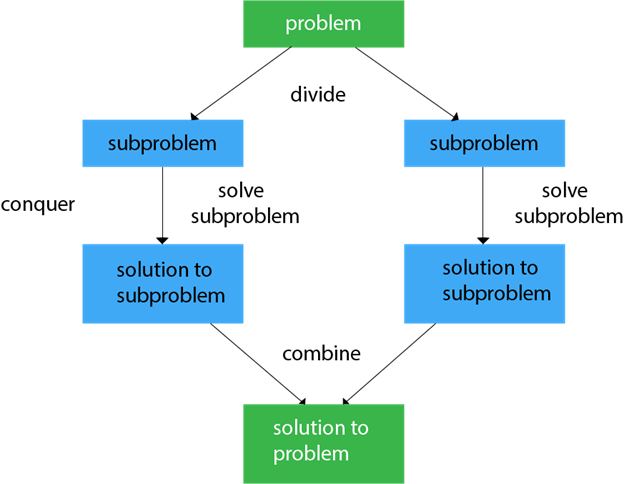
In the picture above, we can notice that the problem is first broken into two sub-problems, further divided into four smaller sub-problems. For example, Once the arrays are broken down to the required number of sub-arrays. These sub-arrays are then solved and merged into larger arrays. This ultimately gives us the solved array.

Merge Sort

Algorithm

Merge Sort is a stable sorting algorithm based on the divide and conquer algorithm. In this algorithm, we first divide the unsorted list of numbers into N sub-divisions. These sub-divisions are then compared and sorted recursively. We then merge the sorted sub-divisions to obtain the sorted list.

Merge Sort, by Wikipedia

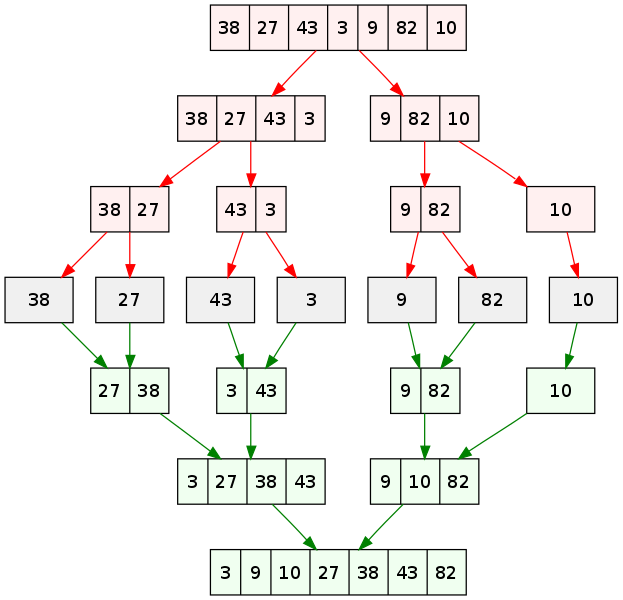
The picture above shows that the original array is divided into two and four smaller arrays. We have now divided the original array of 7 elements into four smaller arrays with two elements in 3 of the arrays and one in the 4th array. We then compare the two elements of the arrays. In this case, we compare 38 and 27, 43 and 3 and 9 and 82. Since ten is in an array of size 1, we take the element as it is. We determine the higher number in each comparison and sort the smaller arrays. We have now obtained sorted smaller arrays which are [27, 38], [3, 43], [9, 82] and [10]. We now compare the elements of the smaller arrays in pairs of two. We compare [27, 38] with [3, 43] and [9, 82] with [10]. After comparing the arrays, we merge the pair to obtain two sorted arrays, [3, 27, 38, 43] and [9, 10, 82]. We now compare these two arrays and merge the arrays to obtain the sorted form of the original array finally. The resulting array is [3, 9, 10, 27, 38, 43, 82].

Complexity and Recurrence Relation

Time Complexity: O(n log(n))

Space complexity: O(n)

Recurrence Relation: T(n) = 2T(n/2) + n

Code

void Sort(A[], B[], n)
{
    CopyArray(A, 0, n, B);
    SplitMerge(B, 0, n, A);
}

void SplitMerge(B[], iBegin, iEnd, A[])
{
    if(iEnd - iBegin <= 1)                      
        return;                                 
    iMiddle = (iEnd + iBegin) / 2;              
    SplitMerge(A, iBegin,  iMiddle, B);  
    SplitMerge(A, iMiddle,    iEnd, B);  
    Merge(B, iBegin, iMiddle, iEnd, A);
}

void Merge(A[], iBegin, iMiddle, iEnd, B[])
{
    i = iBegin, j = iMiddle;
 
    for (k = iBegin; k < iEnd; k++) {
        if (i < iMiddle && (j >= iEnd || A[i] <= A[j])) {
            B[k] = A[i];
            i = i + 1;
        } else {
            B[k] = A[j];
            j = j + 1;
        }
    }
}

void CopyArray(A[], iBegin, iEnd, B[])
{
    for(k = iBegin; k < iEnd; k++)
        B[k] = A[k];
}

Importance of Divide and Conquer Algorithm

Advantages

The divide and conquer algorithm is widely used in computer science. It is instrumental in solving many complex problems by breaking down the problem.

The Tower of Hanoi problem is one of those problems. The pain usually consists of 3 pegs and N number of discs. Each disc is of a different size, and we are assigned to move all the discs from Peg 1 to Peg 3 in the same order as it was on Peg 1, which is most prominent on the bottom and most minor on top. We solve this problem using the divide and conquer algorithm.

Let us assume N to be 3 in our example. We first move the smallest disc from Peg 1 to Peg 3. We then transfer the middle disc to Peg 2. Then, we carry the smallest disc to Peg 1 and the giant disc to Peg 3. Now we have discs [Smallest, Middle] in Peg 2 and Largest in Peg 3. We now move the smallest disc back to Peg 1 and the middle disc on top of the giant disc in Peg 3. We finally move the smallest disc on top of the middle disc on Peg 3. We have achieved our goal of moving all the discs in order in Peg 3.

Divide and conquer algorithms are also used in executing multi-processor machines and using memory caches.

Implementation

1. Merge Sort
2. Quick Sort
3. Karatsuba Algorithm
4. Strassen’s Algorithm6
5. Computing Discrete Fourier Transform
6. Syntactic Analysis

Summary

The Divide and Conquer algorithm is a fundamental algorithm in computer science. The algorithm helps programmers in solving complex problems faster and more efficiently. It is easy to make our programs more quickly and more optimised.